Do You Draw Arrows At The End Of A Line Of Best Fit

Physics Practical Skills Part four: Drawing graphs and lines of all-time fit

In part 4 of the Physics Skills Guide, we explain how to draw a line of best fit correctly in Physics Practicals. Read the postal service to learn virtually dos and don'ts of drawing a line of best fit.

Introduction to Cartoon Graphs and Lines of Best Fit

In this Guide, nosotros explicate the importance of scientific graphs in Physics and how to draw scientific graphs correctly including lines of best fit. This is a really important Physics skill and you'll need to master it if yous want to ace your next Physics Practical test.

In this article nosotros hash out:

• Scientific graphs
• Drawing the line of all-time fit
• Common mistakes with drawing lines of best fit

Want to ace your adjacent Physics Practical Assessment?

Learn how to:

• Assess the validity, reliability and accurateness of whatsoever measurements and calculations
• Determine the sources of systematic and random errors
• Identify and apply appropriate mathematical formulae and concepts
• Draw appropriate graphs to convey relationships

with the Matrix Practical Skills Workbook.

Sharpen your Physics skills

Get exam-ready for your Physics practical assessments with this free prac skills workbook.

Your workbook is on the way! Cheque your electronic mail for the downloadable link. (Please permit a few minutes for your download to land in your inbox)

DOWNLOAD YOUR FREE SKILLS WORKBOOK

Scientific Graphs

What are scientific graphs?

A graph is a visual representation of a relationship between two variables, x (the contained variable) and y (the dependent variable).

Graphs go far piece of cake to place trends in data that you have collected and can be analysed in order to perform a calculation or a measurement, related to addressing the aim of an experiment.

How to draw a scientific graph

Step	Action	Detail
1	Place the variables	Identify your independent variable on the x-axis of your graph and the dependent variable on the y-centrality.
two	Make up one's mind the variable range	Subtract the lowest data value from the highest information value
three	Determine the scale of the graph	Determine a calibration, (the numerical value for each square or sectionalisation), that best fits the range of each variable. Use a calibration that allows your data to be graphed as large as possible in the space provided. The range of each axis may be different. They exercise not demand to start at zero but it is recommended every bit this allows yous to extrapolate if needed. The scale of each axis may be different, buteach one must exist consequent. If one partitioning represents ane metre at the starting time of the graph on one axis, i segmentationalways represents one metre on that centrality.
4	Number and label each axis	Clearly characterization the 10 and y-axes including the units of each measurement.
5	Plot the information points	Plot each data value on the graph with a cantankerous (x)
6	Draw the graph	Place a tendency or a human relationship betwixt the independent and dependent variables. Remove whatsoever outliers from consideration. Describe a curve or a line that best describes the identified trend. Well-nigh graphs of experimental data in Physics are linear and not drawn as "connect­ the ­dots". Just describe the line (or curve) over the range for which you lot have information. Do not extend your line beyond this range. If required to extrapolate (extend the graph along the same slope beyond the range of data), use a dotted line to indicate that yous are extrapolating.
7	Provide a descriptive title	Your title should clearly communicate what the graph is near. Do not simply restate what is already shown on the axes.

In Twelvemonth 11 and 12 Physics, the trends that you will investigate are generally linear, or can be converted into linear graphs, and, hence, you'll be required to draw a line of best fit.

Drawing the line of best fit

An example of a correctly drawn line of best fit is shown below, along with an incorrect i:

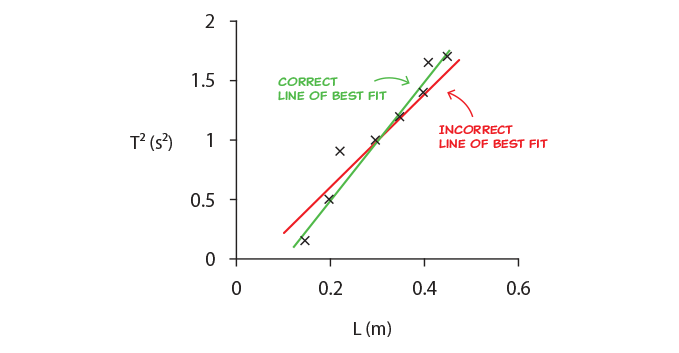
How to draw a line of best fit

To depict the line of best fit, consider the following:

• Outliers must be ignored.
• The line must reflect the trend in the data, i.east. it must line up best with the majority of the data, and less with data points that differ from the bulk.

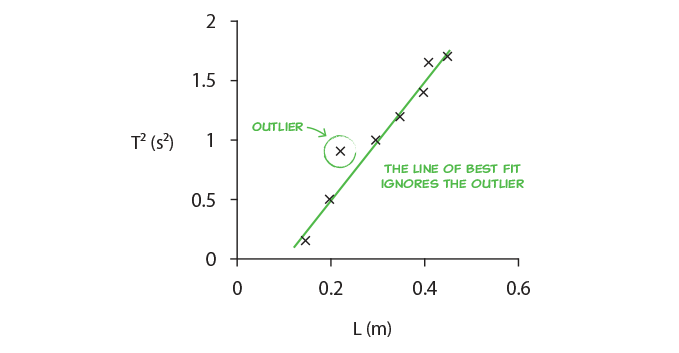
• The line must exist balanced, i.e. it should have points above and below the line at both ends of the line.

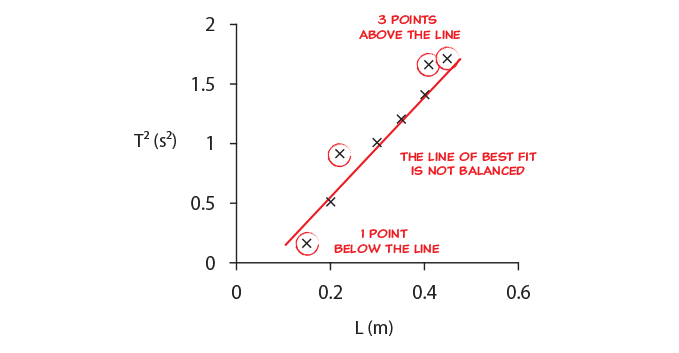
• Do Non force the line to laissez passer through whatever specific data points, or to pass through nada. The purpose of the line of best fit is to reveal the trend of all the data.

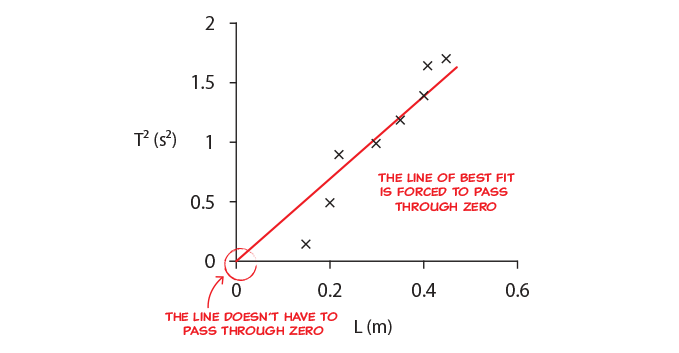
Why do we need to draw a line of best fit?

The master reasons for drawing a line of best fit are to:

• Reduce the effect of both systematic and random mistake and thus make the experiment more accurate and more reliable.
• Find and utilize the gradient of the line of best fit to determine an unknown in the experiment. Ordinarily determining this unknown addresses the aim in some way

How does the line of all-time fit reduce experimental errors?

Past drawing the line of best fit we are looking for the strongest trend in the data, and in this manner reduce the effect of random errors. If nosotros then use the gradient of the line of best fit we expect at differences in values rather than accented values, which reduces or eliminates the upshot of systematic errors.

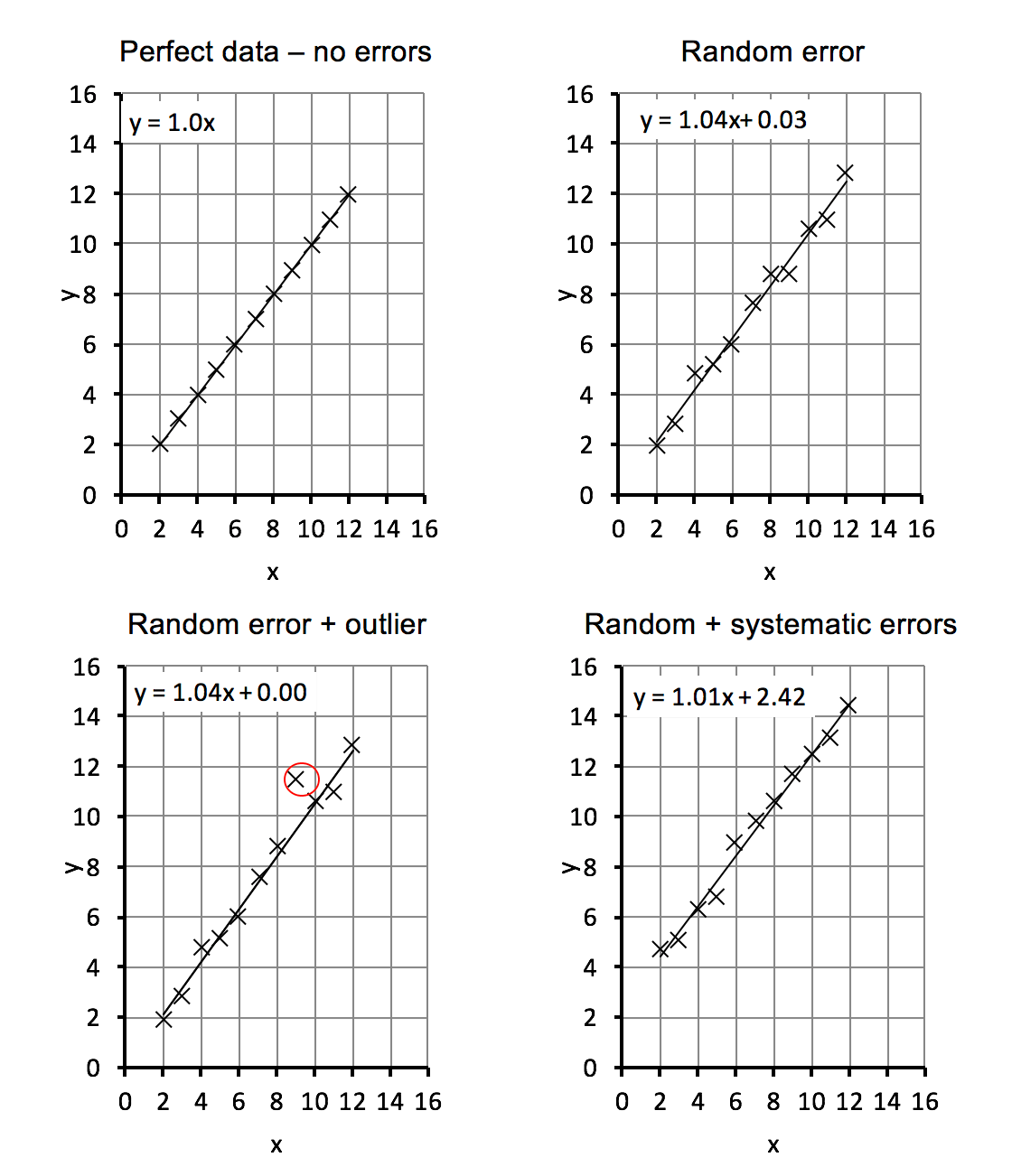
The graphs below illustrate four examples with different types of errors and with no errors:

1. Perfect information with no errors
2. Random error
3. Random error with outlier
4. Random and systematic errors

The gradient represents the result of the experiment and should have a value of ane, so the equation of the line is \(y=x\).

How does using a line of best fit reduce experimental errors?

Using a graph gives results that are as expert or meliorate than calculating from the data points direct and then averaging, as shown in the table below.

Types of error present	Effect obtained from the gradient of a line of best fit	Result obtained from computing using all information points and averaging them
Perfect data – no errors	one.00	1.00
Random error	1.04	1.04
Random error with outlier	ane.04	ane.07
Random and systematic errors	ane.01	ane.47

From the table, we tin can run across that:

• The perfect data has a gradient of 1.
• The random error gives a gradient is 1.04, still very shut to the correct value of 1.
• The outlier is ignored by the line of best fit, so the gradient is still 1.04, close to the correct value. Averaging over the data points would not ignore the outlier and would give a worse result of one.07.
• The systematic error shifts up the information by the same corporeality but does not change the gradient, which is still 1.01. This is withal very shut to the correct value of 1.Still, averaging over the points, in this case, gives an incorrect answer of i.47.

Common mistakes with drawing lines of best fit

The example beneath shows mutual mistakes by students when drawing lines of best fit. The exact mistakes the students have fabricated are listed below.

Mistake 1: Missing labels

Graph i shown beneath is missing labels:

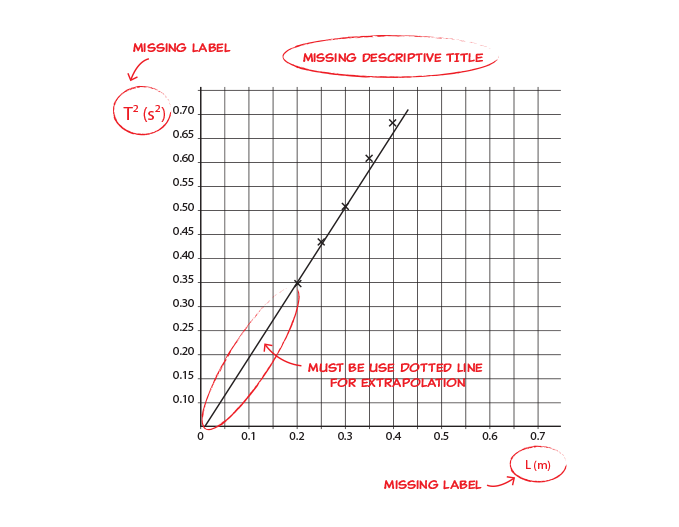
Mistakes in this graph include:

• Missing labels for the axes
• Missing descriptive title
• The extrapolated line is not drawn using a dotted line

six Common Mistakes HSC Physics Students Make in Exams

Mistake 2: Incorrect scale

Graph 2 shown beneath contains an incorrect calibration:

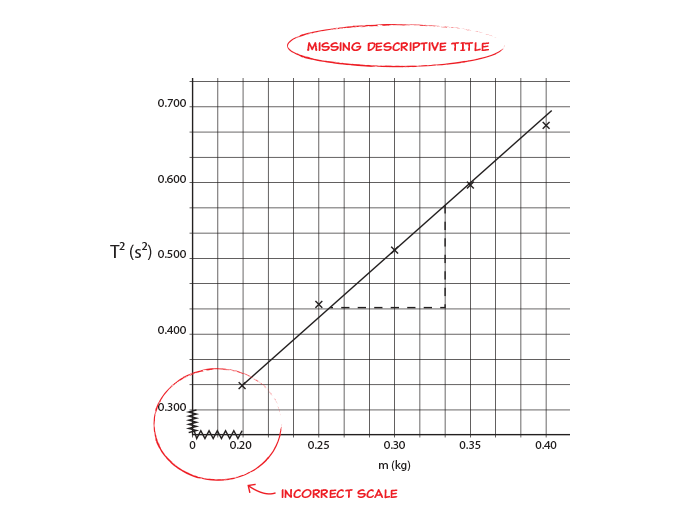
Mistakes in this graph include:

• Incorrect calibration in ten and y-axes. Each segmentation should represent the same value across each axis. For instance, if each segmentation is set a value of 0.05 at the start of the graph for that axis, then i sectionalisation should always represent 0.05 for that axis.
• The student should either start the calibration at 0 or at 0.20 on the x-axis.

© Matrix Education and www.matrix.edu.au, 2022. Unauthorised employ and/or duplication of this material without express and written permission from this site's writer and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and articulate credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.

More Essential Guides

Go costless study tips and resources delivered to your inbox.

Join 75,893 students who already accept a head first.

Source: https://www.matrix.edu.au/the-beginners-guide-to-physics-practical-skills/physics-practical-skills-part-4-how-to-draw-a-line-of-best-fit/

Posted by: johnsonyousterromme.blogspot.com

Share this post